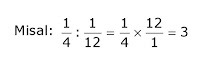Rata-rata, Modus, Median dan Quartil

Rata-rata, modus, median, quartil adalah istilah yang digunakan dalam statistika. Statistik merupakan hal yang berkaitan dengan data dan penyajian data. Penyajian data statistik  dapat dilakukan dengan cara:

1. Tabel, cara penyajian data dalam bentuk baris dan kolom
2. Diagram batang cara penyajian data dalam sebuah diagram yang berbentuk batang atau balok
3. Diagram garis, cara penyajian data dalam bentuk garis
4. Diagram lingkaran, penyajian data dalam bentuk lingkaran yang dibagi beberapa bagian 
5. Poligon atau histogram, merupakan bagian yang menyajikan data dalam bentuk batang seperti halnya diagram batang namun data yang satu dengan yang lainnya dibuat tidak terpisah dan Poligon adalah diagram garis yang menyatakan data dalam bentuk garis yang dihubungkan antarnilai tengah setiap data yang berada diatas histogram.   

• Rata-rata atau mean adalah jumlah semua data di bagi banyaknya data

        

• Modus (Mo) adalah data yang sering muncul atau dat yang memiiki frekuensi  paling tinggi
• Median atau nilai tengah suatu data yang telah di urutkan dari nilai terkecil sampai dengan nilai terbesar
• Quartil adalah nilai yang membagi data yang sudah berurutan menjadi empat bagian yang sama sehingga akan terdapat tiga nilai yang disebut:

1). Quartil 1 (Q₁) atau Quartil bawah

Jika n ganjil: Q₁ – data ke ¼ (n + 1 )

Jika n genap: Q₁ – data ke ¼ (n + 2)

2). Quartil 2 (Q₂) atau Quartil tengah atau median

Jika n ganjil: Q₂ – (n + 1 ) : 2

Jika n genap:  Q₂ – ½ [n/2 +( n/2 + 1)]

3). Quartil 3 (Q₃) atau Quartil atas

Jika n ganjil: Q₃  – ¾ (n + 1)

Jika n genap:  Q₃  – ¼  (3n + 2)

Contoh Soal

• Nilai Ujian tengah semester Ani pelajaran agama 80, IPS 85, IPA 75, matematika 86, dan bahasa Inggris 74. Berapakah nilai bahasa Indonesia Ani jika rata-rata nilai adalah 80. 

Pembahasan: Langkah pertama: Jumlahkan nilai yang telah diketahui: 80 + 85 + 75 + 86 + 74 = 400. Langkah kedua: 80 x 6 (jumlah seluruh mata pelajaran) = 480. Jadi,  nilai bahasa Indonesia Ani adalah 480 - 400 = 80. Atau bisa juga dengan cara: 80  (Rata-rata) x 5 (jumlah mata pelajaran yang telah diketahui) = 400. Kemudian 80 x 6 (jumlah seluruh mata pelajaran) = 480 - 400 = 80

• Berdasarkan pengambilan data berat badan anggota PMI Palembang diperoleh data berikut: 76, 52, 48, 82, 60, 62, 71, 59, 57, 83, 75, 71, 61, 60, 57, 49, 52, 59, 49, 74. Berapakah nilai mediannya? 

Pembahasan: Urutkan nilai dari yang terkecil sampai tertinggi: 48, 49, 52, 52, 57, 57, 59, 59, 60, 60, 61, 62, 71, 71, 74, 74, 75, 76, 82, 83. Median terletak pada data ke 10 dan ke 11. Maka: (data ke 10 + data ke 11) : 2 = (60 + 61) : 2 =  60,5

• Berikut ini data nilai matematika suatu kelas 7, 8, 6, 7, 7, 8, 5, 8, 7, 6, 9, 7, 8, 8, 7, 6, 9, 4, 7, 8. Berapakah rata-rata nilai matematika kelas tersebut? 

Pembahasan: Rata-rata = (7+8+ 6+ 7+ 7+8+ 5+ 8+ 7+ 6+ 9+ 7+ 8+ 8+ 7+ 6+ 9+ 4+7+ 8) : 20 = 142 : 20 = 7,1 

• Suatu kelas terdapat 20 siswa yang memiliki rata-rata tinggi badan 161 cm. Budi adalah siswa baru, kemudian dihitung tinggi badan siswa menjadi 162 cm. Berapakah tinggi badan Budi?

Pembahasan: 

162 cm = (20 x 161) + T_Budi : (20 + 1) 

162 x 21 = 3220 + T_Budi 

_{3402        =} 3220 + T_Budi 

T_{Budi =} 3402 - 3220 = 182 cm

Demikianlah uraian singkat mengenai Rata-rata, Modus, Median dan Quartil, semoga bermanfaat!!!

Read More

Perbandingan

Perbandingan terbagi menjadi dua jenis yaitu:

1. Perbandingan senilai merupakan perbandingan dua variabel (variabel A dan variabel B) yang apabila dibagi atau dikali dengan bilangan yang sama, maka besarnya perbandingan tetap. Artinya semakin besar nilai A maka semakin besar pula nilai B begitupun sebaliknya semakin kecil nilai A maka semakin kecil pula nilai B.
2. Perbandingan berbalik nilai merupakan perbandingan dua variabel (variabel A dan variabel B). Semakin besar nilai A maka semakin kecil nilai B begitupun sebaliknya semakin kecil nilai A maka semakin besar nilai B.

Berikut gambaran mengenai dua jenis perbandingan tersebut: 

Selanjutnya, jika terdapat nilai perbandingan seperti berikut ini maka berlaku: 

 Contoh Soal Perbandingan:

1). 40 pekerja dapat menyelesaikan pekerjaan dalam waktu 8 hari, jika ada 8 orang tidak masuk kerja maka mereka dapat menyelesaiikan pekerjaan tersebut dalam waktu berapa hari?

a. 10 Hari 

b. 11 Hari

c. 12 Hari

d. 13 Hari

e. 15 Hari

Pembahasan:

40 Pekerja = 8 Hari

40-8 pekerja =..... Hari

Karena ini merupakan perbandingan berbalik nilai, maka: P1/P2 = H/8

40/32 = H/8

Kemudian dikali silang (40 x 8) : 32 = 10 Hari.

2) Suatu pekerjaan diselesaikan oleh 24 orang dalam waktu 20 hari. Jika pekerjaan tersebut dipercepat penyelesaiannya selama 15 hari, maka tambahan pekerja yang diperlukan adalah...

A. 6 orang

B. 8 orang

C. 18 orang

D. 32 orang

E. 36 orang

Pembahasan:

P1 = 24

T1 = 20 Hari

T2 = 15 hari

P2= .... ?

Karena ini merupakan perbandingan berbalik nilai. Maka: 24/x = 15/20

15x = 24 x 20

X = (24 x 20) : 15 = 32 orang.

Jadi, tambahan pekerja adalah 32 - 24 = 8 orang.

3). Umur Sifa dengan kakaknya 5 : 9. Selisih umur mereka 20 tahun. Berapakah umur mereka masing-masing?

A. Umur Sifa 25 tahun dan umur kakanya 35 tahun

B. Umur Sifa 25 tahun dan umur kakanya 45 tahun

C. Umur Sifa 35 tahun dan umur kakanya 45 tahun

D. Umur Sifa 40 tahun dan umur kakanya 50 tahun

Pembahasan:

Sifa = 5 / (9-5) x 20 = 25

Kakak = 9 / (9-5) x 20 = 45

4). Jika harga 12 buah mangga Rp. 60.000 berapakah harga 9 buah mangga?

A. 120.000

B. 65. 000

C. 45. 000

D. 30. 000

Pembahasan:

12 / 60.000 = 9 / x

X = (60.000 x 9) : 12 = 45.000

5). Siswa SMA dan SMP mengikuti ujian matematika dalam satu gedung. Jika seorang siswa SMP keluar gedung maka 1/7 yang ada digedung adalah siswa SMP. Jika dua orang siswa SMA keluar gedung maka 1/5 siswa yang ada digedung adalah siswa SMP. Berapakah perbandingan siswa jumlah SMP dan SMA? 

 A. 9 : 2

B. 7 : 4

C. 9 : 3

D. 4 : 2

Pembahasan:

SMA + SMP = X

Jumlah SMA = Y

1/7  (X-1) = Y -1

X = 7Y - 7 +1

X = 7Y - 6

1/5 (x - 2) = y

x - 2  = 5y

x = 5y + 2

Masukan nilai x

 7y - 6 = 5y + 2

2y = 8

y = 8 : 2 = 4 

Masukan nilai y

x = 5y + 2

x = 5(4) + 2 = 22

SMA + SMP = X

SMA + 4 = 22

SMA = 22 - 4 =18

Jadi, perbandingan siswa SMP : SMA adalah 4:18 atau 2 : 9

Read More

Untung, Rugi, Bruto, Netto, Tara, Diskon

Untung dan Rugi

Dalam suatu transaksi jual beli akan menghasilkan untung dan rugi. Untung akan didapat apabila harga penjualan lebih besar daripada pembelian. Sedangkan rugi terjadi jika harga pembelian lebih besar daripada penjualan.

Rumus: Untung = Harga Jual – Harga Beli

Rumus: Rugi = Harga Beli - Harga Jual

Bruto, Netto, Tara, Diskon

1. Bruto adalah berat kotor suatu barang yaitu berat isi (barang) ditambah dengan berat kemasan atau media.
2. Netto adalah berat bersih suatu barang
3. Tara adalah berat kemasan atau media suatu barang
4. Diskon (rabat) adalah potongan harga terhadap suatu barang dan biasanya dinyatakan dalam persen {%)

Rumus:

Bruto = Netto + Tara

Netto = Bruto – Tara

Tara = Bruto – Netto

Diskon = Persentase {%) Diskon  x Harga Jual Awal

Satuan Berat

1 Ton            :1000 kg

1 Kwintal       :100 kg

1 Kg               :10 Ons

1 Pon            : 5 Ons

1 Ons            :100 gram

Contoh Soal

1. Sri membeli tas di sebuah toko dengan harga Rp 200.000 jika tas yang hendak dibelinya mendapatkan diskon sebesar 20% dan karena sri memiliki kartu member maka ia mendapat potongan lagi sebesar 5%. Berapakah harga tas yang harus dibayar oleh Sri?

Pembahasan

Harga Awal Rp 200.000

Diskon 20% + diskon member 5% = 25%. Maka 25/100 x 200000 = 50.000

Jadi, harga tas yang harus dibayar Sri adalah Rp 200.000 – 50.000 = Rp.150. 000.

2. Ani membeli motor baru dengan harga Rp. 17.000.000 dan di jual lagi dengan harga Rp. 18.360.000. Berapa persen keuntungan yang didapatkan Ani?

Pembahasan:

Untung = 18.360.000 - 17.000.000 = 1.360.000

Persentase (%) = 1.360.000 / 17.000.000 x 100% = 8%. Jadi, Ani mendapatkan keuntungan sebesar 8%.

3. Andi membeli suatu barang dengan harga Rp. 20.000 dan dijual dengan mendapatkan keuntungan 20% harga penjualan tersebut berapakah harga jual barang tersebut?

Pembahasan:

Harga Jual = (100% + 20% ) x 20.000

Harga jual = 120% x 20.000 = 24. 000

Atau bisa juga menggunakan rumus:

Harga jual = 20.000 + (20% x 20.000) = 24. 000

4. Sebuah AC terjual dengan harga Rp. 1.800.000, jika penjual mengalami kerugian 10%. Berapa harga pembelian AC tersebut?

Pembahasan

karena persebtase kerugian telag ditentukan maka, 

Harga jual = Persentase beli - persentase rugi = 1.800.000

Harga jual = 100% - 10% = 1.800.000

Harga Jual = 90/100 = 1.800.000

Jadi harga beli 2.000.000 karena dikalikan silang 100 x 1.800.000 : 90 = 2.000.000. 

Demikianlah penjelasan singkat mengenai untung rugi, semoga bermanfaat!!!

Read More

Waktu, Jarak Dan Kecepatan

A. Waktu

Waktu adalah lama berlangsungnya suatu kejadian. Satuan waktu yang paling sering digunakan adalah detik, menit, jam. Selain itu, ada juga hari, minggu, bulan, tahun, dan lainnya tergantung dari keadaan pertanyaannya. Biasanya satuan antara pertanyaan dan jawaban yang dibutuhkan berbeda, sehingga kita perlu mengkonversinya terlebih dahulu agar satuannya menjadi sama. Untuk itu, kita juga perlu mengetahui hubungan antara suatu satuan waktu dengan satuan waktu yang lainnya.

Berikut ini beberapa satuan waktu yang sering muncul:

1 menit = 60 detik

1 jam = 60 menit = 3.600 detik

1 hari = 24 jam

1 tahun = 12 bulan = 52 minggu = 365 hari

1 triwulan = 3 bulan

1 caturwulan = 4 bulan

1 semester = 6 bulan

1 tahun = 12 bulan

1 lustrum = 5 tahun = 60 bulan

1 windu = 8 tahun = 96 bulan

1 dekade = 10 tahun = 120 bulan

1 abad = 10 dasawarsa = 100 tahun

1 masehi = 1 milenium = 1000 tahun.

Rumus Waktu untuk menyusul (arah sama)

Rumus Waktu untuk berpapasan (arah berlawanan)

B. Jarak

Jarak adalah angka yang menunjukkan seberapa jauh suatu benda berubah posisi melalui suatu lintasan tertentu. Satuan yang paling umum digunakan adalah satuan panjang meter (m), namun kembali kepada pertanyaannya sehingga kita juga harus mengkonversi satuannya terlebih dahulu bila diperlukan. Dibawah ini adalah gambar yang menjelaskan hubungan antar satuan panjang. Berikut ini satuan jarak;

Dari tangga diatas maka kita dapat mengambil beberapa contoh hubungan antar satuan panjang berikut:

1 km = 10 hm = 100 dam = 1000 m

1 m = 10 dm = 100 cm = 1000 mm

1 m = 0,001 km

1 mm = 0,000001 km

Dengan memahami konsep dari tangga diatas, maka kita dapat dengan mudah mengkonversi satuan panjang tanpa perlu menghapal satu per satu.

C. Kecepatan

Kecepatan merupakan besaran yang menunjukkan seberapa cepat suatu benda berpindah dari satu tempat ketempat lainnya dengan satuan waktu tertentu. Dari pengertian tersebut terlihat bahwa kecepatan dapat diukur dengan menggunakan komponen jarak yang dibandingkan dengan waktu. Sehingga satuan kecepatan berupa jarak/waktu. Misalnya km/jam, meter/detik, dan lainnya.

Rumus Kecepatan Rata-Rata:

Hubungan Waktu (T), Jarak (S) dan Kecepatan (V) dapat dirumuskan:

Jika ditanya waktu maka rumusnya adalah jarak : kecepatan. Jika ditanya jarak maka rumusnya adalah kecepatan x waktu.

Resultan waktu dan kecepatan

Jika t1 adalah waktu yang dibutuhkan orang pertama untuk menyelesaikan sebuah pekerjaan, t2 adalah waktu yang diperlukan oleh orang kedua untuk menyelesaikan pekerjaan yang sama, dan orang berikutnya, maka resultan waktu jika mereka mengerjakannya bersama-sama adalah: 

Jika v1 adalah kecepatan orang pertama untuk menyelesaikan sebuah pekerjaan, v2 adalah kecepatan orang kedua untuk menyelesaikan pekerjaan yang sama, dan orang berikutnya, maka resultan kecepatannya adalah sebagai berikut:

Contoh Soal :

1. Si Lisa dan si Mirna memiliki pekerjaan sebagai asisten rumah tangga. Waktu yang dibutuhkan oleh si Lisa dalam mencucui piring adalah 30 menit, sedangkan waktu yang dibutuhkan si Mirna adalah 60 menit. Jika si Lisa dan si Mirna bekerja bersama-sama dalam mencuci piring tersebut, maka waktu yang dibutuhkan adalah ...

Pembahasan:

2. Jarak kota A dan B adalah 120 km. Jika x = lama waktu tempuh dari A ke B dengan kecepatan 75 km/jam, dan y = lama waktu tempuh dari A ke B dengan kecepatan 30 m/s, maka ...

a. x < y

b. x = y

c. x > y

d. 2x > y

e. hubungan x dan y tidak dapat ditemukan

Pembahasan:

3. Seorang anak bernama Intan setiap pagi selalu berolah raga memutari sebuah lapangan dengan keliling 0,5 km. Apabila dengan kecepatan lari 5 km/jam Intan mampu memutari lapangan sebanyak 5 kali, berapa lamakah Intan lari setiap paginya ?

a. 10 menit

b. 30 menit

c. 50 menit

d. 40 menit

e. 20 menit

Jawab:

Setiap hari Intan berlari dengan jarak 2,5 km (0,5 x 5)

waktu= jarak/kecepatan= (2,5 km)/(5 km/jam)=0,5 jam

maka Intan setiap hari berlari selama 30 menit.

4. Seorang anak bernama Intan dalam 1 menit dapat membuat 10 simpul pita, sedangkan Joko dapat membuat dua kali lipatnya. Jika Intan mulai bekerja 15 menit lebih awal dari Joko, dan keduanya selesai setelah Joko bekerja selama 1 jam maka banyak simpul yang dihasilkan keduanya adalah ...

a. 450

b. 1950

c. 2700

d. 2250

e. 1800

Jawab :

Stotal = SIntan + SJoko

Stotal = (10 x 75 menit) + (20 + 60 menit) = 1.950

5. Jika sebuah benda bergerak dengan kecepatan delapan kaki perdetik, berapakah jarak yang ditempuhnya selama setengah jam ? (1 kaki = 0,3048 meter)

a. 4,39 kilometer

b. 8,78 kilometer

c. 43,9 meter

d. 438,9 centimeter

e. 1440 meter

Jawab :kecepatan = 8 kaki/detik

waktu = 30 menit = 1800 detik

jarak = kecepatan x waktu

jarak = 8 x 1800 = 14.400 kaki = 4.389 meter = 4,39 kilometer

6. Bani bersepeda dari kota X ke kota Y dengan kecepatan 40 km/jam kemudian kembali lagi ke kota X dengan kecepatan 20 km/jam. Jika x adalah kecepatan rata-rata bersepeda Bani dan y=26 2/3 km/jam maka ...

a. x > y

b. x < y

c. x = y

d. hubungan antar x dan y tidak dapat ditentukan

jawab;

Read More

Hitung Cepat

Hitung Cepat merupakan salah satu Tes Numerik Aritmetika. Tes ini bertujuan untuk mengetahui kemampuan seseorang dalam berhitung dengan cermat dan benar dalam waktu yang terbatas. Umunya soal yang diujikan dalam hitung cepat adalah penjumlahan, pengurangan, pembagian, perkalian, pecahan, persentase, perbandingan, rata-rata, jarak, waktu dan kecepatan.

Aturan dasar Aritmetik adalah sebagai berikut:

• Urutan Operasi Hitung yang di dahulukan adalah angka yang ada dalam tanda kurumg - angka berpangkat/akar – perkalian/ pembagian – penjumlahan/pengurangan.
• Penjumlahan/pengurangan pecahan harus menyamakan penyebut terlebih dahulu

• Pembagian dengan pecahan adalah sama dikalikan dengan kebalikan dari pecahan pembagi (pembilang dan penyebut dibalik)

• Perkalian/pembagian tanda sejenis menghasilkan tanda positif
• Perkalian/pembagian tanda berbeda jenis menghasilkan tanda negatif

Jenis-jenis Bilangan

Pecahan

Pecahan adalah suatu bilangan yang terdiri dari pembilang dan penyebut dengan bentuk a/b. Pecahan terbagi menjadi beberapa jenis:

• Pecahan biasa, yaitu dengan bentuk a/b dengan a, b, adalah elemen bilangan bulat dan b tidak sama dengan 0. 
• Pecahan campuran,  contoh
• Pecahan desimal merupakan bentuk lain dari suatu pecahan yang ditandai dengan ciri koma. Pecahan desimal juga termasuk bentuk pecahan yang penyebutnya angka 10, 100, 1000, dan seterusnya. Contoh:
• Pecahan persen yaitu bentuk lain dari pecahan dengan penyebut 100 dan dapat ditulis dengan a % artinyan a/100
• Pecahan perseribu atau permil yaitu pecahan dengan penyebut 1000 dan dapat ditulis %₀ atau b %₀  artinya b/1000.

Operasi Hitung Pecahan

• Penjumlahan dan pengurangan. Untuk pecahan desimal, operasi penjumlahan dan pengurangan dilakukan dengan mensejajarkan posisi koma. Jika pecahan yang dijumlahkan memiliki penyebut yang sama maka dapat langsung dijumlahkan dengan ketentuan hanya pembilangnya saja yang dijumlahkan dan penyebut tetap. Contoh:

 

• Perkalian. Operasi perkalian ada pecahan dilakukan dengan mengalikan pembilang dengan pembilang dan penyebut dengan penyebut. Pada pecahan desimal perkalian dapat dilakukan seperti perkalian biasa tetapi jumlah angka dibelakang koma merupakan jumlah angka dibelakang koma yang dikalikan. Contoh:

 

• Pembagian. Operasi pembagian pecahan dilakukan dengan cara mengalikan pecahan dengan kebalikan pecahan pembaginya. Contoh:

• Perpangkatan. Contoh:

• Akar. Contoh: 

Persentase Dalam Pecahan

Persentase adalah pecahan yang penyebutnya 100. Untuk mengubah bentuk persentase menjadi pecahan yaitu dengan menuliskan bilangan asli sebagai pembilang dan 100 sebagai penyebut. Jenis soal persentase pecahan yang sering muncul yaitu:

1. Hasil 25% dari 200 adalah...

2. Persentase nilai 80 dari 640 adalah...

3. 15% dari suatu bilangan adalah 60. Berapakah nilai bilangan tersebut....

Berikut ini angka numerik yang saya rekomendasikan untuk dihapalkan:

 Demikianlah pembahasan mengenai hitung cepat kali ini. Semoga bermanfaat!!!

Read More

DERET ANGKA

Pengertian Deret Angka

Deret angka adalah penjumlahan suku-suku dari barisan tertentu. Contoh: 1+2+3+4+5..., sedangkan barisan adalah susunan dalam bilangan yang dibentuk menurut suatu pola urutan tertentu. Misalnya: 1, 2, 3, 4, 5, ....

Jenis Deret

• Satu Deret, merupakan sebuah deretan angka dengan pola yang dapat ditentukan oleh operasi aljabar anatara satu suku dengan suku berikutnya.
• Dua Deret, merupakan sebuah deretan angka yang ditandai dengan tidak adanya hubungan antara suku satu dengan suku berikutnya.

Tipe Deret

1. Dari segi Larik /baris, terdapat empat macam yakni

• Satu larik ialah sebuah deret yang memiliki satu pola bilangan dan hubungan antar sukunya dapat ditentukan karena hanya satu pola
• Dua larik ialah sebuah deret yang memiliki dua pola yang berbeda karena dibagi menjadi dua sub deret. Misalnya pola larik pertama suku genap, dan pola larik kedua suku ganjil.
• Tiga Larik ialah sebuah deret yang memiliki 3 pola berbeda disetiap lariknya
• Empat larik ialah sebuah deret yang memiliki 4 larik dengan pola berbeda.

2. Fibonacci, yaitu sebuah deret yang memiliki ciri nilai pada suku berikutnya merupakan penjumlahan dua suku sebelumnya.

Contoh Soal Deret:

Bilangan yang tepat untuk mengisi titik-titik pada deret berikut ini

• 7, 10, 13, 16, 19, 22, ... 

Jawaban: 25, pola bilangan tersebut adalah ditambah 3, (Contoh deret satu larik).

• 12, 9, 9, 8, 6, 7, ..., ...,

Jawaban: 3, 6. Bilangan ini termasuk deret dua larik. Larik pertama terdiri dari 12, 9, 6 (pola bilangan tersebut adalah dikurang 3) dan Larik kedua terdiri dari 9, 8, 7, (pola bilangan tersebut adalah dikurang 1).

• 42, 13, 19, 49, 19, 19, 56, 25, 19, ..., ...,

Jawaban: 63, 31. Bilangan ini termasuk deret tiga larik. larik pertama terdiri dari 42, 49, 56, 63 (pola bilangan tersebut ditambah 7), larik kedua terdiri dari 13, 19, 25, 31 (pola bilangan tersebut ditambah 6) dan larik ketiga adalah 19.

• 2, 2, 4, 6, ..., ...., 26, 42

Jawaban: 10, 16. Bilangan ini termasuk deret Fibonacci penjumlahan dua suku bilangan sebelunya (4+6, 10, 16 (10+6)).

Dalam penerapan soal-soal deret terkadang kita dihadapkan dengan soal deret yang bentuknya cerita. Seperti diminta untuk mencari suku ke-n, terkadang juga diminta untuk mencari jumlah suku dari suatu bilangan.

Rumus Suku ke-n:  U_n = a + (n -1) b

Keterangan:

U_n = adalah suku ke-n

a = suku pertama atau U₁

n = banyaknya suku pada barisan

b = beda suku pertama dengan suku ke-dua/suku selanjutnya.

Rumus jumlah suku 

 Keterangan:

S_{n = Jumlah semua anggota deret/ jumlah seluruh bilangan}

a = suku pertama atau U₁

n = banyaknya suku pada barisan

b = beda suku pertama dengan suku ke-dua/suku selanjutnya.

U_n = adalah suku ke-n.

• Suku ke-n (Un) bila Sn diketahui;

 

• Suku tengah (Ut)

Jika diantara dua suku barisan aritmatika disisipkan k buah suku sehingga membentuk barisan aritmatika baru maka beda barisan aritmatika setelah disipkan k buah suku akan berubah.

b’ = beda barisan yang baru

k = banyak suku yang disisipkan

• Banyak suku dari barisan aritmatika yang disisipkan k buah suku juga akan berubah;

n’ = banyak suku barisan aritmatika baru

Tips dan Trik

• Perbanyak berlatih soal, agar semakin banyak variasi pola yang kita ketahui.
• Biasanya pola yang dujikan bukan pola sederhana, tetapi pola yang unik sehingga dibutuhkan kreatifitas dalam pengerjaannya.
• Cermat dan teliti. Terkadang kita melihat seolah ada dua jawaban yang memungkinkan padahal sebenarnya hanya ada satu jawaban yang benar.
• Jangan terlalu berpikir rumit. Terkadang kita langsung memikirkan suatu pola yang rumit pada suatu soal, padahal polanya sangat sederhana.
• Biasanya tingkat kerumitan soal bertambah pada soal-soal akhir.
• Kerjakan soal yang kita anggap mudah terlebih dahulu.

Demikianlah pemaparan singkat mengenai Deret, semoga bermanfaat!!!

Read More